Statistical Methods
Five statistical methods for identifying collocation are available in this
program. They are Dunning's log likelihood, (pointwise) mutual information,
chi-square, cubic association ratio (MI3), and Frager and McGowan coefficient.
(See Manning and Schütze, 1999 and Oakes 1998, for more details)
1. Dunning's log likelihood :
The test compares two hypotheses about W1 and W2
Hypothesis 1 : P(w2|w1) = p = P(w2| not w1)
Hypothesis 2 : P(w2|w1) = p1 not equal
p2 = P(w2|not w1)
Assuming binomial distribution, the log likelihood ratio is calcuated
as follows:
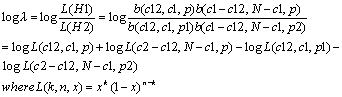
Note that c1 is the frequency of W1, c2 is the frequency of W2, c12
is the frequency of bigram W1-W2, N is the number of total words in the
corpus, p = c2/N, p1 = c12/c1, and p2 = (c2 – c12) / (N-c1).
The higher the value, the more likely that W2 is the collocation of W1.
To see the statistical significance, multiply the result by -2, and
consult the Chi-square table at the degree of freedom as one.
2. Pearson's Chi-square
Collocation between W1 and W2 is calculated in according to the frequency
of bigram occurences in each cell. "W1 - W2" represents the number of occurences
that W1 - W2 is found in the corpus. "not W1 - W2" represents the number
of occurences that the preceding word of W2 is not W1. "W1 - not W2" represents
the number of occurences that W1 is not followed by W2. "not W1 - not W2"
represents the rest.
| W1 - W2 |
not W1- W2 |
| W1 - not W2 |
not W1 - not W2 |
Chi-square is calculated using the formula below, where Oi,j is the
observed frequency in the table, and Ei,j is the expected frequency in
each cell when W1 - W2 occur together by chance. Expect frequency on each
cell is equal to (row total * column total ) / grand total
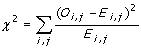
The higher the number, the more significant of collocation between
W1 and W2.
3. Mutual Information
This statistical method compare the probability of finding the two words
together to the probability that the two words are independent to each
other. If x' and y' and collocation, it is likely that P(x' y') be highly
greater than P(x') * P(y'). Thus, the higher the value, the more likely
that the two words are collocation.
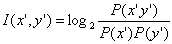
However, mutual information tends to give high value for rare events.
For example, when W1 and W2 always occur together, MI will be higher if
the frequency is lower.
When calculating statistical values for 3-,4-,5-words, pseudo-bigram
transformation is used
to estimate the value. (Silva and Lopes, 1999).
References
-
Manning, Christopher and Hinrich Schütze. 1999. Foundations of Statistical
Natural Language Processing. Cambridge: MIT Press.
-
Oakes, Micheal P. 1998. Statistics for Corpus Linguistics. Edinburg University
Press.
-
Silva, Joaquim Ferreira da, and Gabriel Pereira Lopes. 1999. A Local Maxima
Method and a Fair Dispersion Normalization for Extraction Multi-word Units from
Corpora. In Proceedings of the 6th Meeting on the Mathematics of Language,
Orlando, July 23-25.
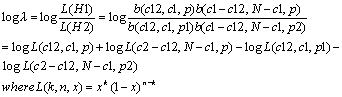
![]()